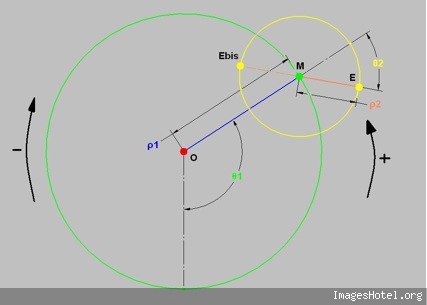
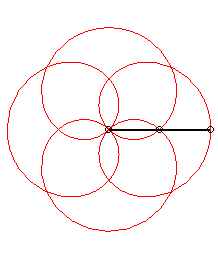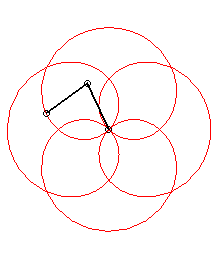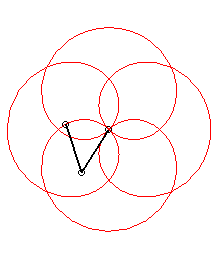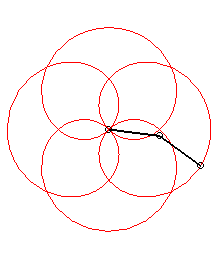
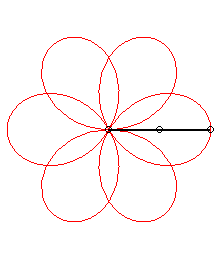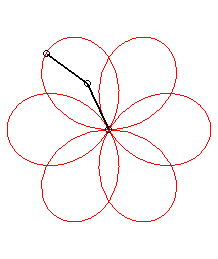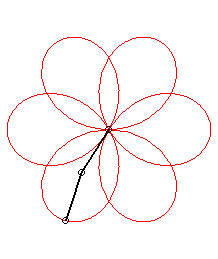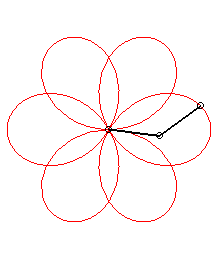
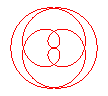
It have been a long time i did not take a look in HOP ... and then i have not exactly caught all the purposes of the previous posts ... so i am just gonna answer the question of the topic ... sorry by advance for the possible repetitions i could make.

So what's that i have called CAPs (Continuous Assembly Patterns) ?!?

Firstly ... let me explain my vision of what a pattern is.

To my mind a pattern is a cyclic curve that can be define in a unique way by its harmonic component (frequencies or number of tours) and by its "modulus" component (radius or lengthes).

In the field of the 2 circles compounds ... which is for instance the most commonly used (i'll explain later the general case of the 3 compounds circles) ... here are some examples according to this model :

O is the shoulder, M is the hand ("Main" in french), E is the Extremity of the object (poď, club staff) and Ebis is the other extremity in the case of the staff.

Theta1 and Theta2 (frequencies or number of turns) define the harmonic part of a pattern whereas Rho1 and Rho2 (radius or length) define the "modulus" part.

Rho=1 when the arm is stretched (when the poď is unwrapped).

The patterns will be defined in the following way : Theta1 Theta2 ; Rho1 Rho2.

And now examples :

The first example is 1 4 ; 1 1 (if E would have run the other way : -1 -4 ; 1 1)
The second example is 1 -6 ; 1 1 (if E would have run the other way : -1 6 ; 1 1)

As we can see these patterns are in a particular case of "modulus" component ... as the 2 radius or lengthes are equal (in this case ... the simplest ... the values are 1) ... and called "rosettes".

There is another particular "modulus" part mode which give curves called cycloďds.
This case happen when the speeds of M and E are equal in the earth (or audience) reference. It means in terms of maths that Rho2/Rho1=abs(Theta1/(Theta1+Theta2)) (Rho1.abs(Theta1)=Rho2.abs(Theta1+Theta2)).

With the first example (1 4 ; 1 1) above it would give us :

And it would be called 1 4 ; 1 1/5.

With the example of a 3 foils "rosette" antispin (1 -3 ; 1 1) :

It would be called 1 -3 ; 1 1/2.

All the cycloids are not feasable ... i mean if we keep the arm stretched (Rho1=1) ... because the differents cases of wraps (thumb excluded) can only take the following values :

Rho2 -> Wrap

1/5 -> 2h+1f
1/4 -> 2h
1/3 -> 1h+3f
2/5 -> 1h+2f
1/2 -> 1h+1f
3/5 -> 4f=1h
2/3 -> 3f
3/4 -> 2f
4/5 -> 1f
1 -> 0f

(h for hand and f for finger)

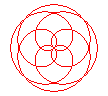
There is also patterns with more than one arm turn (Theta1>1) ... the most popular example of these kind of pattern would be :

AKA 2 -5 ; 1 1 and 2 -5 ; 1 2/3 (if we keep the same sense of running as the examples above)

But there is a lot of other examples like:

AKA 3 2 ; 1 1 and 3 2 ; 1 3/5 (rotated by 90° in this image)

AKA 3 4 ; 1 1 and 3 4 ; 1 3/7 (typical case of unfeasable cycloid ; rotated by 45° in this image)

In general ... with poïs ... all inspins patterns are feasable whereas antispin patterns have a rule of feasability : abs(Theta1)